The Imaging Whiteboard is done. I’ve added every feature I can think of, fixed every bug I know about. 3.0.5 is the final version.
So, what is the next project?
Obviously, I asked ChatGPT.
Me:
“My name is Steve Weavers; my personal web site is http://sound-analysis.com/ . I am responsible for The Musicians Workbench and The Imaging Whiteboard. I have just completed the Imaging Whiteboard. I am looking for ideas for my next project. What do you think I should tackle?”
Here is what it said:
“Hi Steve! It’s great to hear that you’ve completed the Imaging Whiteboard. As for your next project, there are many directions you could go in. Here are a few ideas to consider:
Music notation software: If you enjoy working on music-related projects, creating a software tool that makes it easier for musicians to notate their compositions could be a valuable resource for the community.
Audio editing software: Building an audio editing software could be a complex but rewarding project. You could focus on a specific niche, such as podcast editing, or create a comprehensive tool that covers all aspects of audio editing.
Virtual instrument plugin: If you have experience with music production software, developing a virtual instrument plugin could be a fun challenge. This could involve creating realistic-sounding emulations of real instruments, or coming up with entirely new and unique sounds.
Music recommendation engine: With so much music available online, it can be overwhelming for listeners to discover new artists and albums. Creating a recommendation engine that uses machine learning algorithms to suggest music based on a user’s listening history could be a valuable tool for music lovers.
Audio analysis tool: Given your background in sound analysis, creating a tool that helps users analyze audio files could be a natural fit. This could involve developing algorithms to identify key features of the audio, such as tempo, key, and tonality.
I hope these ideas give you some inspiration for your next project!”
Me:
“Those were excellent suggestions. Do you have any ideas for imaging projects?”
“Certainly, here are some ideas for imaging projects you could consider:
Image recognition software: Developing software that uses machine learning algorithms to recognize and identify objects within images could be a valuable tool for a range of industries, from healthcare to security.
Image processing software: Creating software that enhances or alters images could be a fun and creative project. You could focus on specific effects, such as color correction or noise reduction, or create a comprehensive tool that covers a range of editing capabilities.
Virtual reality experiences: With the increasing popularity of virtual reality technology, creating immersive visual experiences could be a rewarding project. This could involve creating 360-degree images or videos, or developing interactive VR games.
Image compression algorithms: Developing algorithms to compress image files without compromising their quality could be a valuable resource for a range of industries, from web development to photography.
Augmented reality applications: Building applications that overlay virtual objects or information onto real-world images could be a fun and innovative project. This could involve creating educational tools or marketing applications for businesses.
I hope these ideas provide some inspiration for your next imaging project!”
That’s brilliant! The Audio analysis tool might be a good challenge. What do you think?
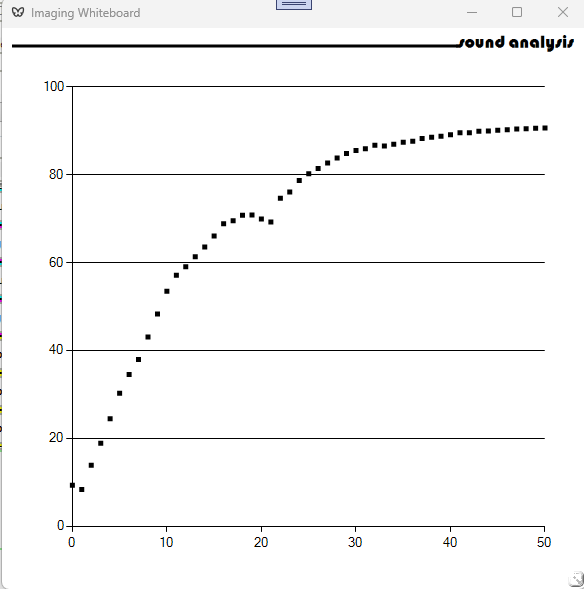
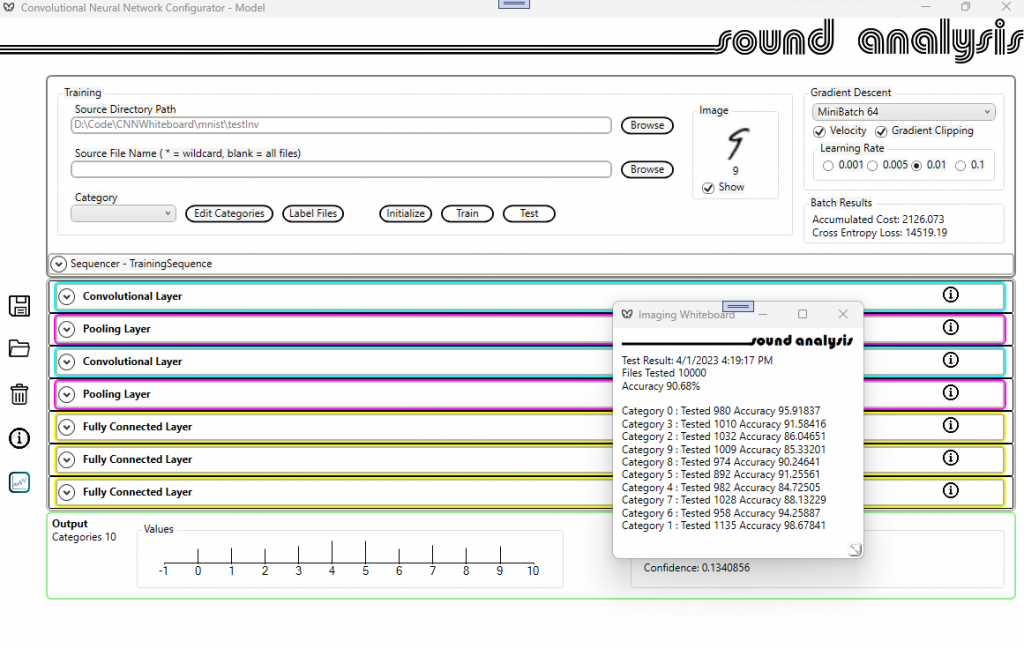
Using the MNIST database of handwritten digits MNIST database – Wikipedia a convolutional neural network was trained to an accuracy of 90%. This took 50 epochs.
The trained model was loaded into the Image Classifier control and used to identify handwritten digits.
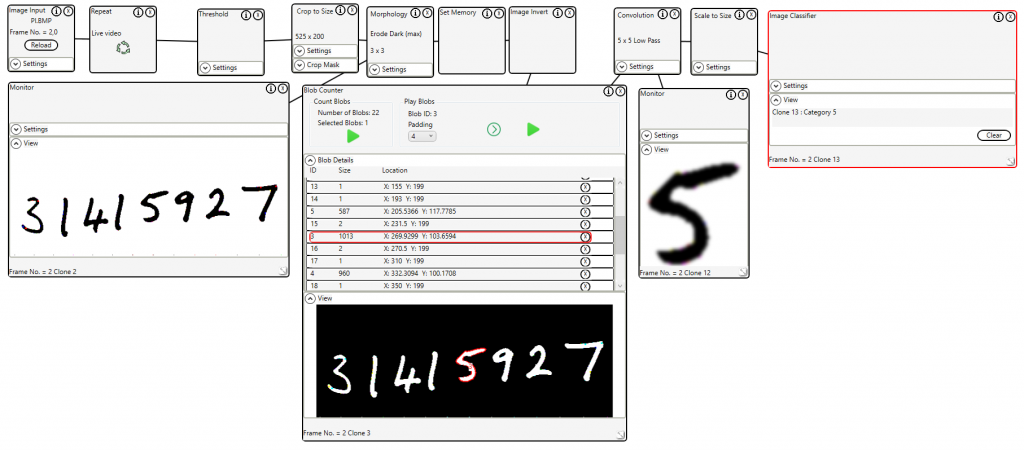
The files required to reproduce this demo are available here https://drive.google.com/file/d/1XKSYvJfAW1maNsaiV0iaWZXor0Tbtuat/view?usp=share_link
The new blob counter control in the Imaging Whiteboard (2.5.7) can be used for more advanced image analysis algorithms.
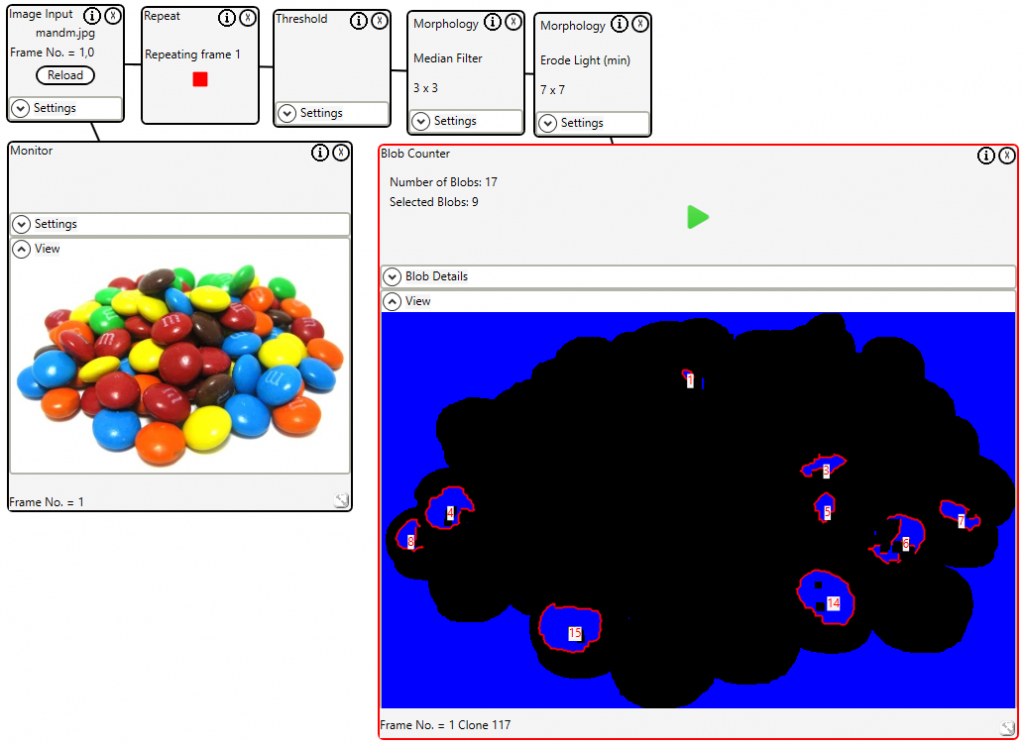
Here we see an image of M&Ms and we want to know how many blue ones are visible. The threshold control is used to separate the blue component of the image. The morphology controls are used to filter out spurious noise and partially visible M&Ms. The blob counter will identify the blobs and allow the user to select the blobs or interest. The selected blobs count is the answer.
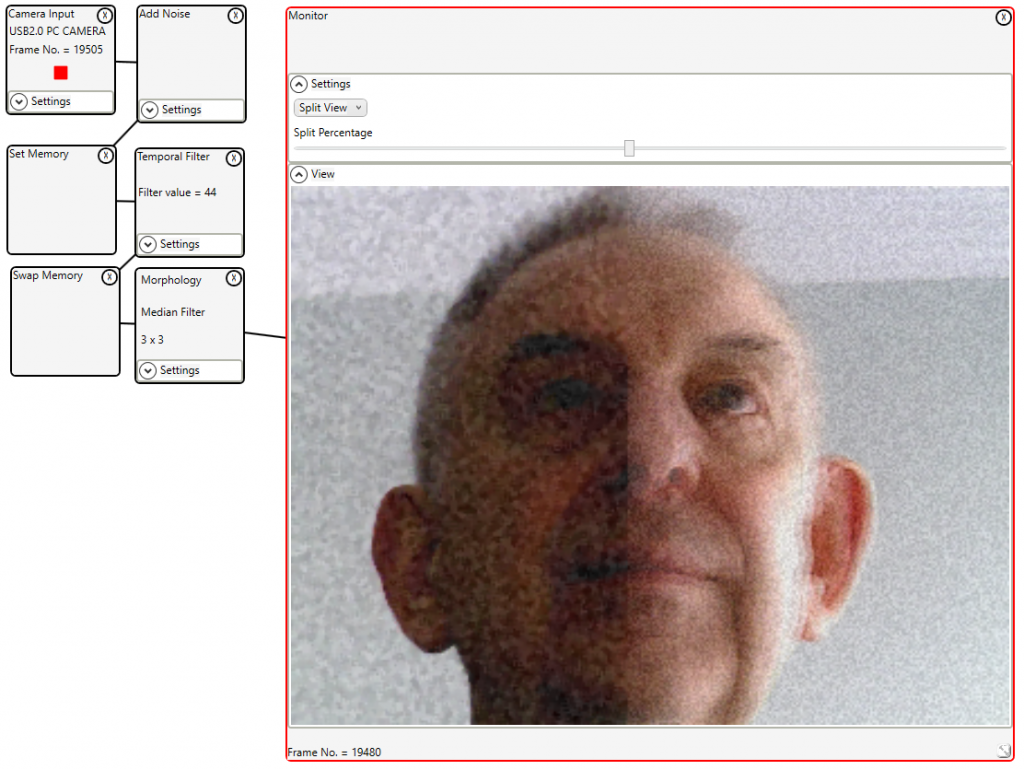
Here we can see the results of two methods applied to the same image shown on the monitor simultaneously. The split screen feature will be available in version 2.5 of the Imaging Whiteboard.
Noise is added to the image and the set memory control will write the noisy image to the secondary memory. The temporal filter is applied to the primary memory. Swap memory switches the primary and secondary memories. The 3×3 median filter is applied. The monitor shows the primary image (morphology result) on the left, and the secondary (temporal filter) on the right.
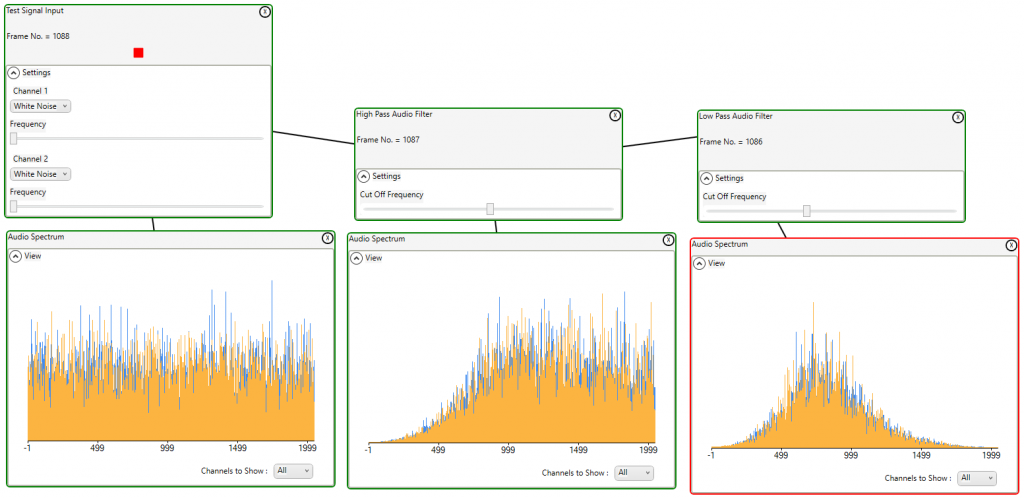
White noise will contain all frequencies. By applying filters to white noise and viewing the resulting spectrum the effects can be viewed. Here we see the test signal generator producing white noise on 2 channels and the resulting spectrum. The high pass filter is applied to the signal and the resulting spectrum with low frequencies eliminated is shown. The low pass filter is then applied eliminating the high frequencies.
Tracking a target in a raw image may not provide the best tracking performance in all cases. Often tracking a target in a processed image is better. The pre-processing may be edge detection such as a Sobel filter (shown here), or setting a threshold, noise filtering etc.
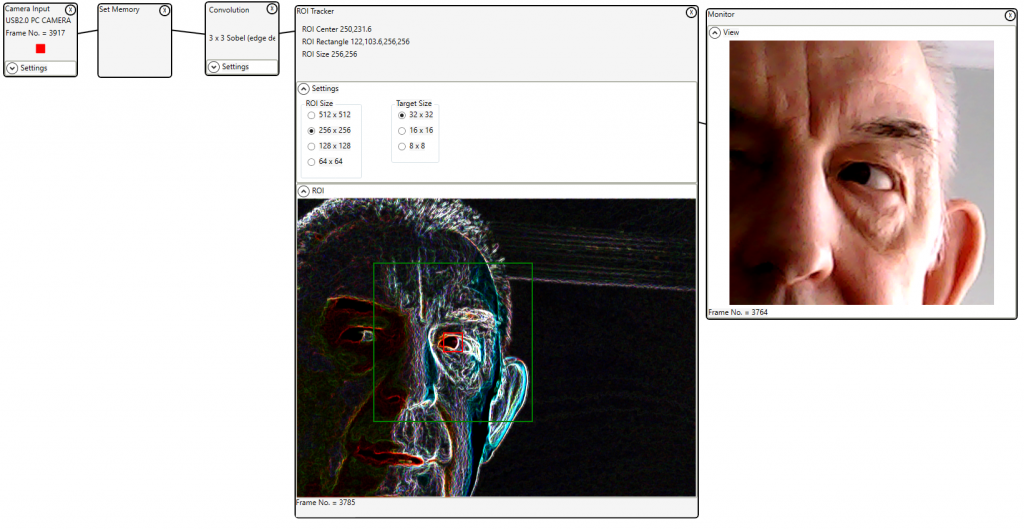
Using the Set Memory control the original image is saved to memory. The pre-processing (convolution) is performed on the main pixels. The target is tracked in the processed image, but the crop that is passed to the next control is extracted from the image in memory (if it exists). The type of pre-processing will vary depending on the video used.
The latest version (2.3.2) released on this web site (not in the MS store yet) has a new “Low Frequencies Center” option added to the FFT filter control. This option is more convenient for common FFT filters.
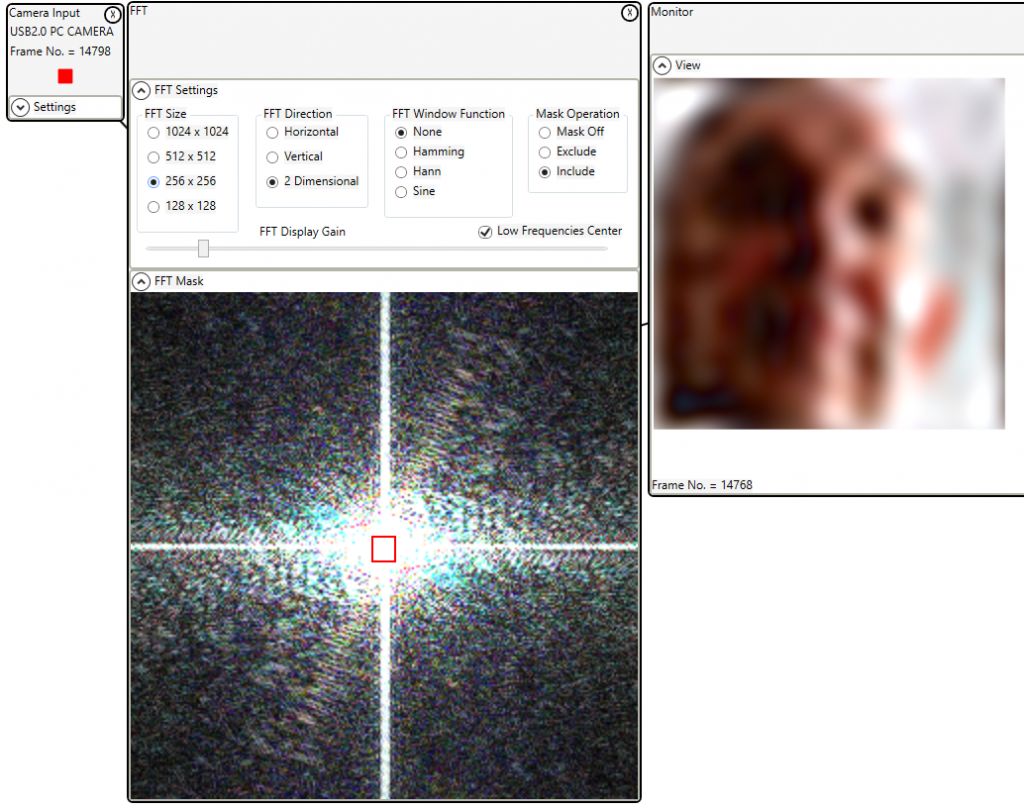
By including the low frequencies in the center of the FFT mask window a low pass filter can be implemented.
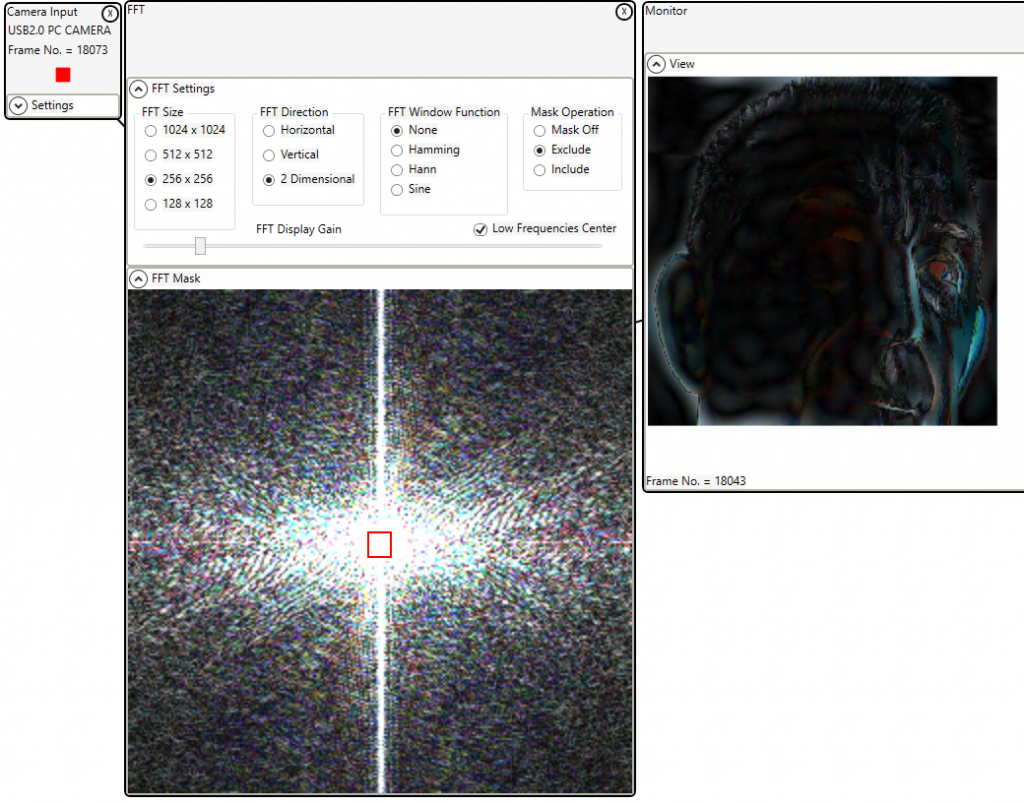
By excluding the same low frequencies a high pass filter can be implemented.
Keeping the resolution low (256×256 in this case) will provide a reasonable live experience; still not quite real-time.
Now that Imaging Whiteboard 2.0 has been released this would be a good time to blog about some of the new features. The Warper has been improved to include variable warps. Previously only fixed warps were implemented; that is warps such as zoom and rotate where the warp factor is the same for every pixel, see previous blog http://sound-analysis.com/using-complex-arithmetic-to-perform-combination-warps/ . Version 2.0 includes variable warps; that is warps where the warp factor is dependent on the target image location (specifically distance from the center of the target image).
Complex number arithmetic is still used, but, the fixed warp factor is split into two components: Fixed Zoom Factor and Fixed Rotate Factor. These are calculated once. Then for each pixel the variable part of the warp factor is calculated from the user input and the target pixel address. The full warp factor is calculated:
(FixedZoomFactor + variableZoom) * (FixedRotateFactor * variableRotate)
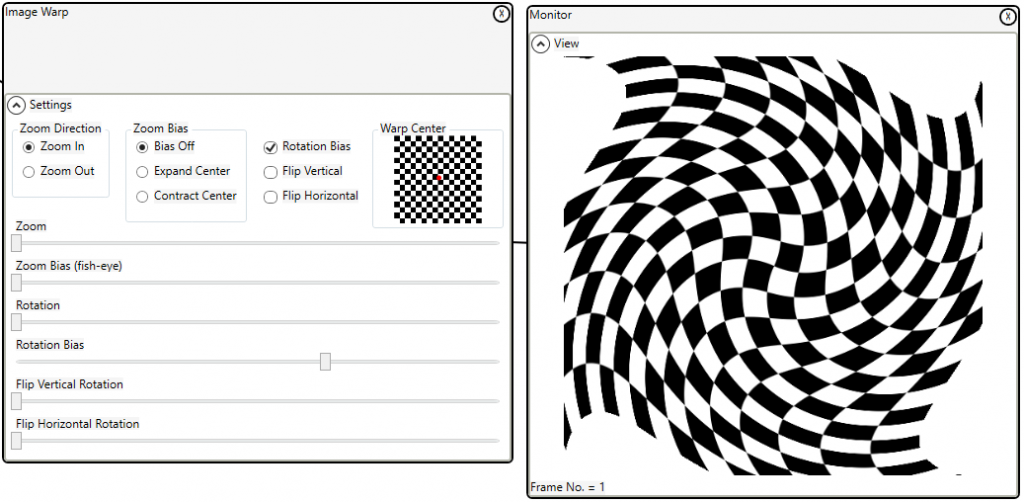
Fish-eye correction can be achieved using the variable zoom. This works well enough, but, is wrong in a number of ways. First it is too simple, real fish-eye correction will take account of the source fish-eye lens properties see Fisheye lens correction (paulbourke.net) if you really want the details. Also, this technique is based on the target pixel location as it implements backward mapped warping (more efficient), real fish-eye correction will use the source image location to determine the correction.
Fish-eye correction is shown in the user manual and further in the cookbook. Here we see biased rotation applied to a chequerboard:
A new control will allow the user to add random noise to the video.
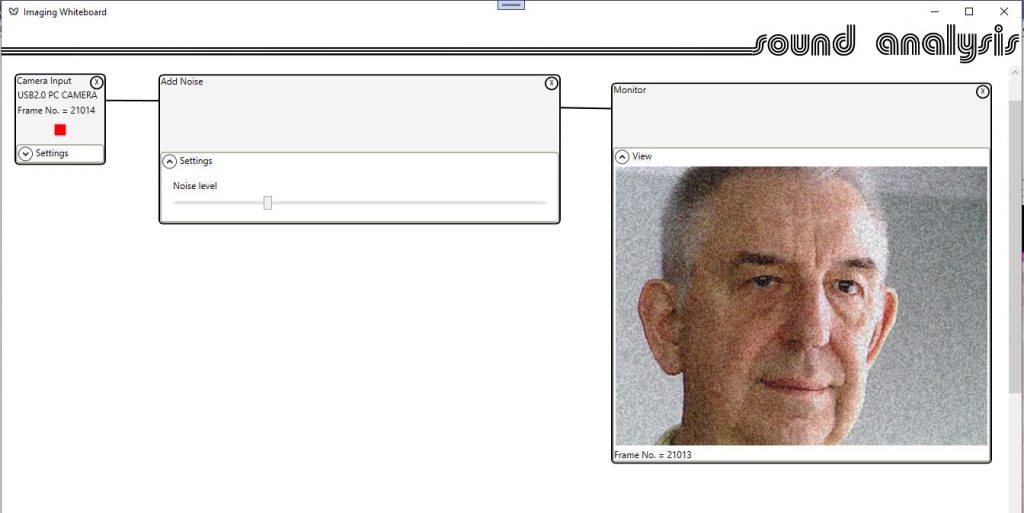
The slider control will modify the amount of noise added from none to only noise.
This control will allow the user to evaluate various noise reduction techniques.
The temporal filter will do a pretty good job with high filter values, but, the problem of movement blurring will be worse at higher levels. This technique is only applicable to video, not single images.
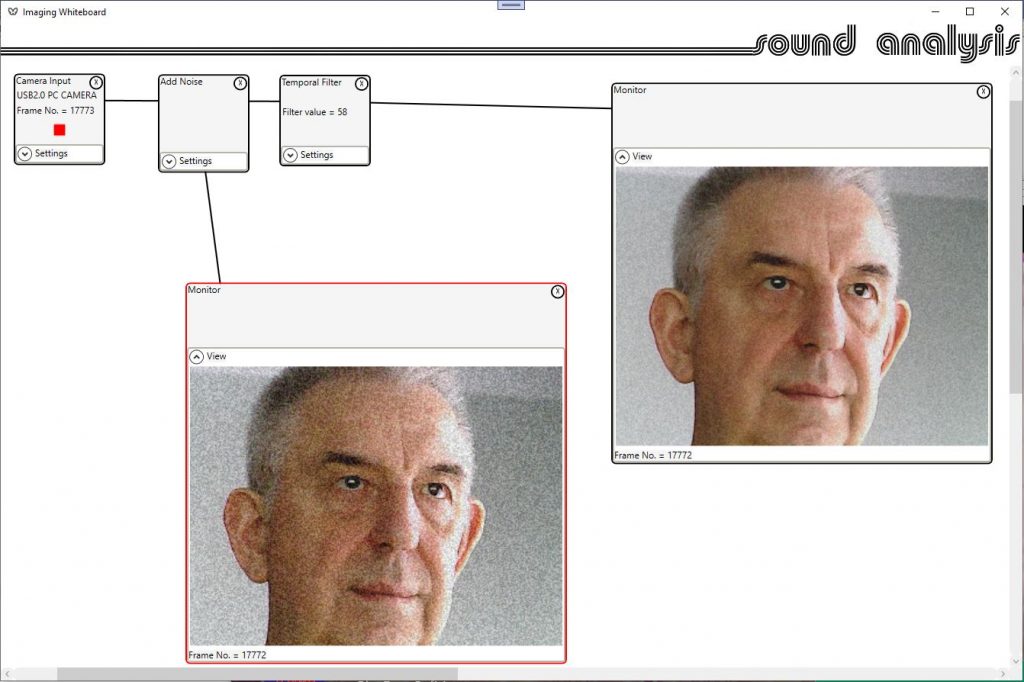
The most obvious spatial technique would be a low pass convolution. This will result in a loss of detail, but is applicable to video or still images.
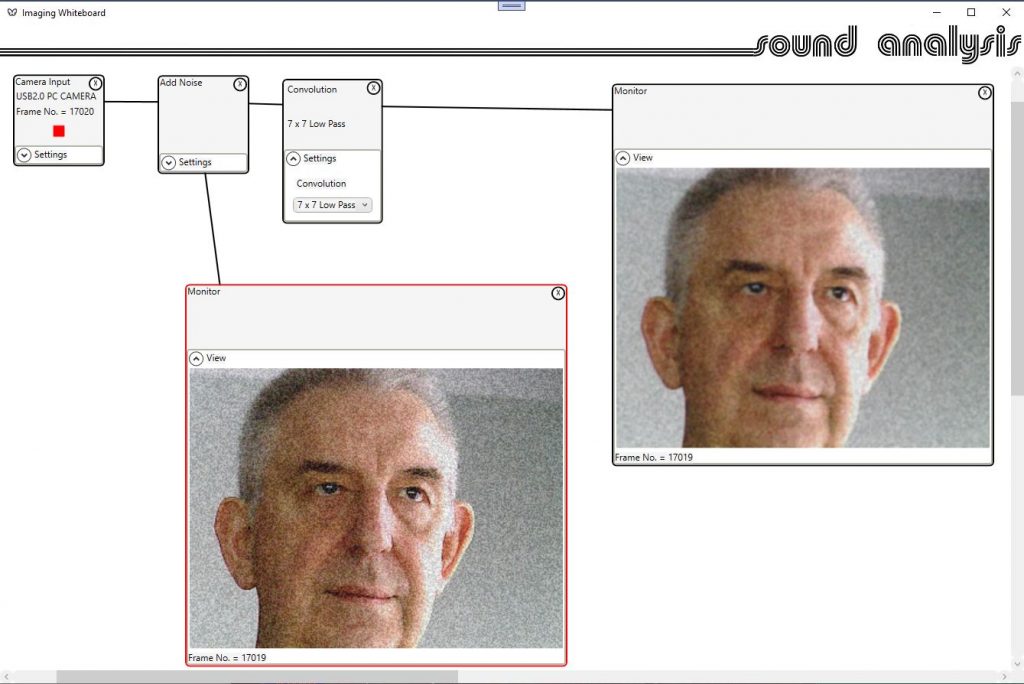
A couple of morphological operations will do a better job of removing noise, but will result in some image blocking.
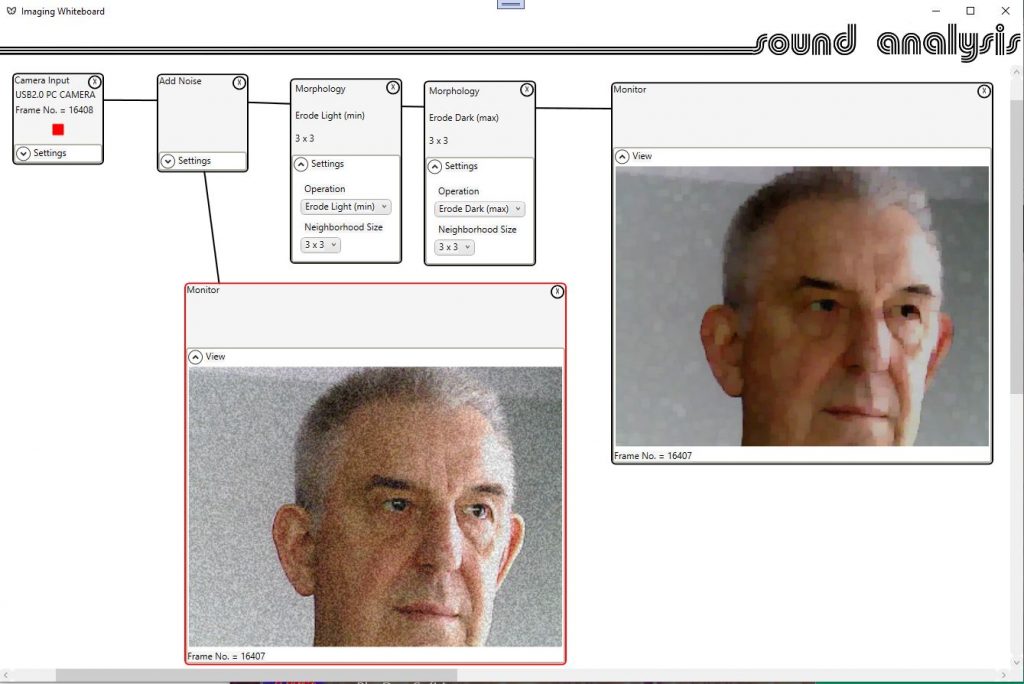
The choice of noise reduction technique will depend on the application, the amount of noise anticipated, and personal taste. The Imaging Whiteboard will now allow the user to experiment with various techniques and combinations; varying the parameters and noise level to find the preferred approach.
The Mandelbrot generator has been added to the Imaging Whiteboard. The whole point of the Mandelbrot is infinite complexity from a simple algorithm. The plot points are generated with only 5 lines of code:
Complex z = new Complex(0.0, 0.0);
Complex c = new Complex(((double)w - MandelbrotSize / 2 +
HOffsetSliderValue) / (ZoomSliderValue * 64),
((double)h - MandelbrotSize / 2 +
VOffsetSliderValue) / (ZoomSliderValue * 64));
uint iteration = 0;
for (; iteration < maxIterations && z.Magnitude < 2; iteration++)
{
z = (z * z) + c;
}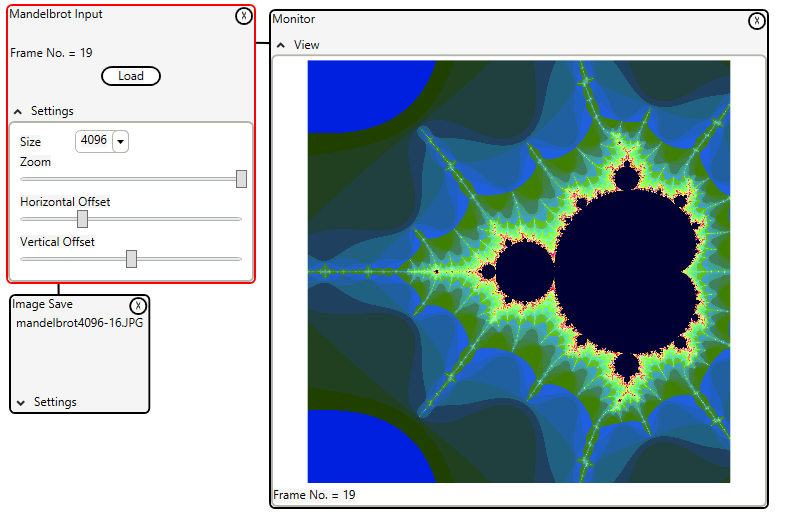
The control allows the user to zoom into details of the Mandelbrot and generate details.
The detail shown above is from the very left tip of the full scan. It seems that this detail repeats the full scan, but, not exactly. At first glance the Mandelbrot seems to contain much repetition; unlike fractals these repetitions are not exact.
The full un-zoomed plot looks like: