I’ve created a channel on YouTube. I’ve posted some short instructional videos to show the basics of the Imaging Whiteboard. There will be more posted soon.
Version 3.5 of the Imaging Whiteboard introduces extended frequency domain processing. The FFT control will now output the FFT results with the output image, a second FFT control will detect the previous results and perform the reverse FFT. Other controls have been extended to support processing these results.
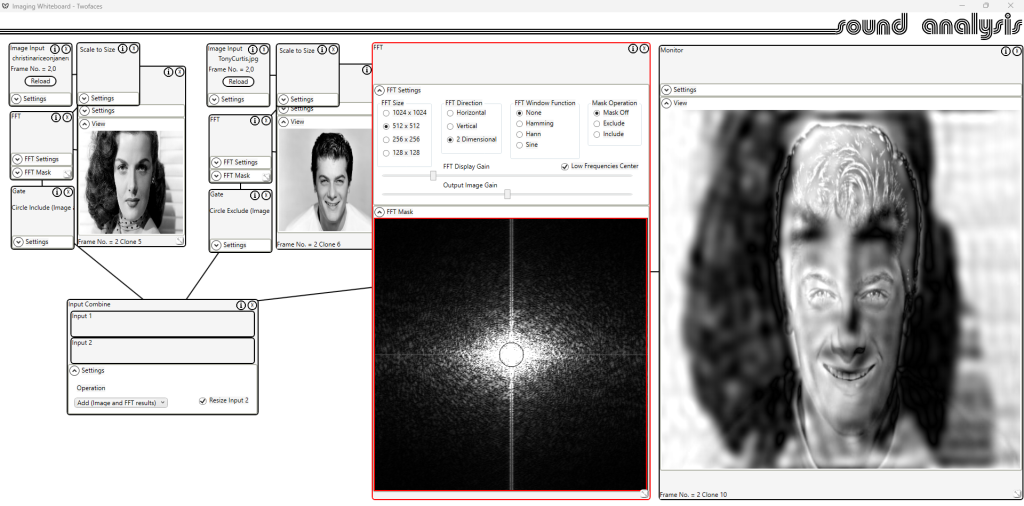
Here an image of Jane Russell has been transformed and the high frequencies excluded. An image of Tony Curtis has been transformed and the low frequencies excluded. The two processed FFT results have been added and the reverse transform performed. When the image is viewed close up the eye sees Tony, from a distance the eye sees Jane.
In the last blog post I showed how the line detector could be used with a Sobel filter. In this post I will show how Canny edge detection https://en.wikipedia.org/wiki/Canny_edge_detector can provide a better input to the line detector.
The latest cookbook http://sound-analysis.com/imaging-whiteboard-3-0/ shows how to use the Line Detector Control with a Sobel filter, and, how to perform Canny edge detection. This post will show how to combine both.
First, we prepare the image; repeat will help making the adjustments to the Canny edge detection, Set region will limit the entire process to a specific region. Monochrome because the Hough transform is a monochrome process.
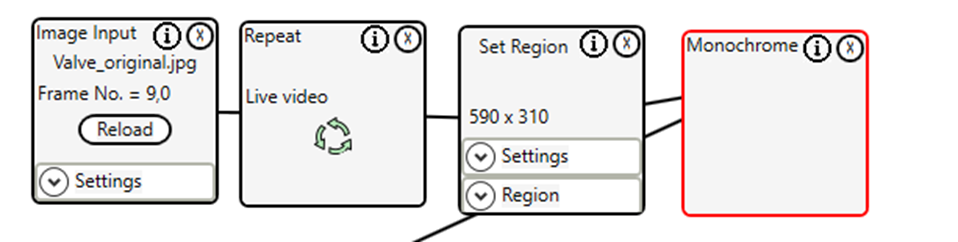
Next, we filter the image to remove noise, and perform the initial edge detection using a full Sobel filter (includes edge direction) and gradient thresholding.
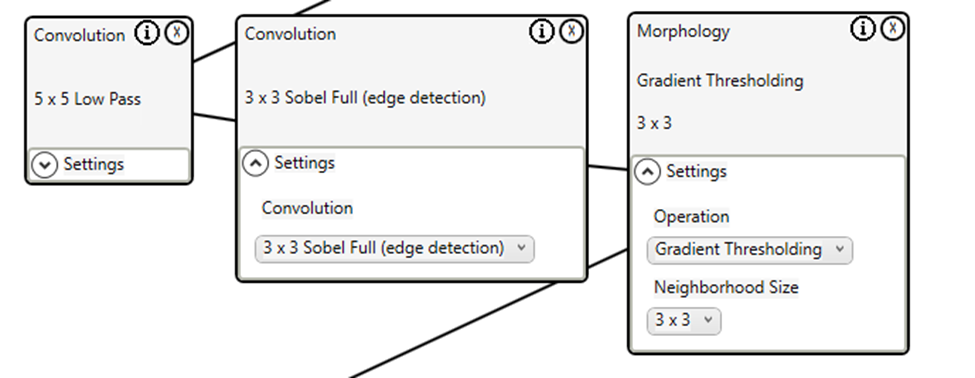
Next, we complete the Canny edge detection with double thresholding and edge hysteresis.
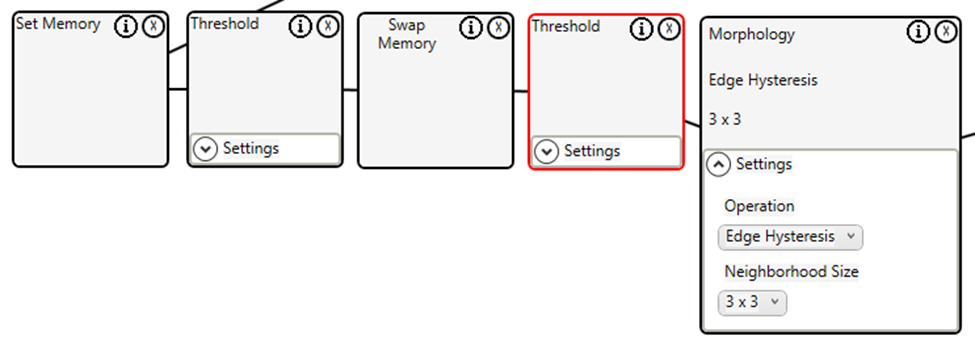
Finally, we use the Edge Detector to identify the most prominent lines.

In version 3.2 of the Imaging Whiteboard a Line Detector control has been added. The line detection is performed using a Hough transform https://en.wikipedia.org/wiki/Hough_transform . The lines detected are defined by the shortest distance from the origin to the line, and the angle between the x axis and the line connecting the origin to the closest point on the line. Theoretically the lines are infinitely long.
Since we want to be able to restrict the Hough transform to a specified region we want to display the detected lines in that region. Without line length restriction the display would look like:
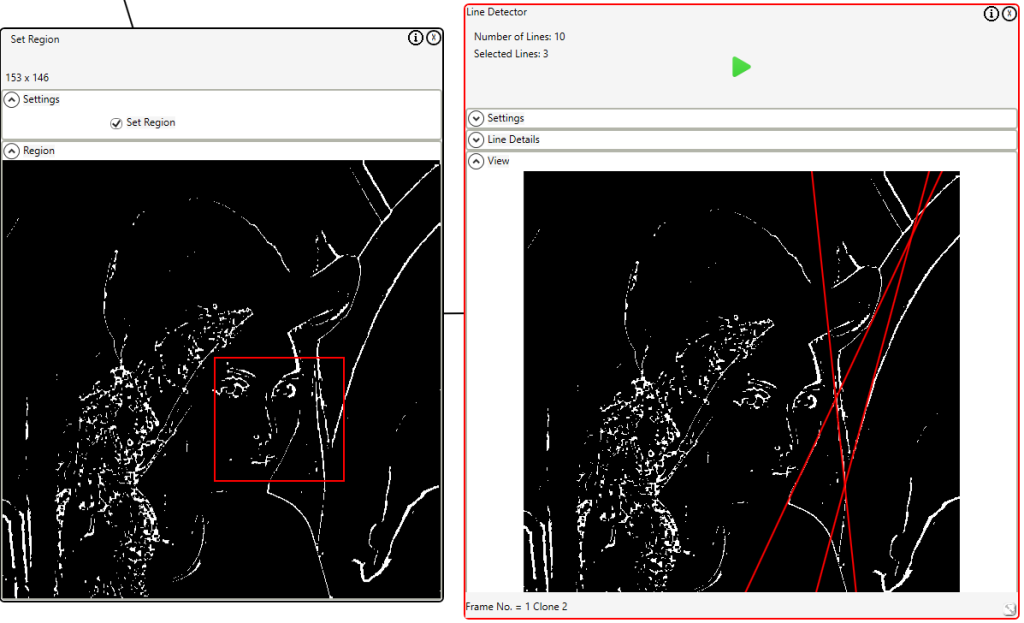
With lines restricted to the specified region the display correctly looks like:

How is this performed? Every point on a line is defined by:
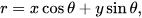
where r is the distance from the origin to the closest point on the straight line, and θ is the angle between the x axis and the line connecting the origin with that closest point.
So for each line the start and end points must be trimmed to lay on the region perimeter. Each point must be trimmed horizontally and vertically. Horizontal trimming looks like:
if (point.X < region.Left)
{
point.X = region.Left;
point.Y = _centerH – (int)((radius – Math.Cos(thetaRadians) * (region.Left – _centerW)) /
Math.Sin(thetaRadians));
}
if (point.X > region.Right)
{
point.X = region.Right;
point.Y = _centerH – (int)((radius – Math.Cos(thetaRadians) * (region.Right – _centerW)) /
Math.Sin(thetaRadians));
}
Vertical trimming is similar. The _centerW and _centerH values exist because the origin is in the center of the image, but, pixel 0,0 is in the top left corner; adjustment must be made before and after the calculation.
Now that the Audiophile’s Analyzer is complete how can all of the features be provided to the Musician’s Workbench?
Simply backporting the code would not be the best solution, it would result in massive code duplication. Even more problematic would be the clash of design philosophies.
The Musician’s Workbench was designed to reproduce the functionality of the original SA-10 hardware. It is lean and real-time by design.
The Audiophile’s Analyzer was designed to provide every known music transcription technique, and to provide it all in a single integrated package. It is large and not real time.
The solution is to allow the Audiophile’s Analyzer to import session files from the Musician’s Workbench.

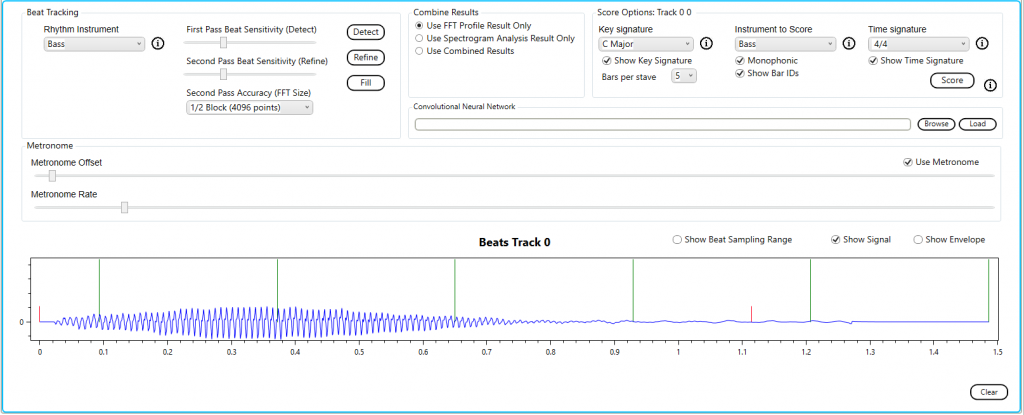
Here we see the Beats graph from the Analysis tab of the Audiophile’s Analyzer. The beats are from the session file, and were originally generated by the metronome of the Musicians workbench. The audio signal is overlaid, this is the original audio sampled by the Musician’s Workbench. The audio was only sampled on the beat when there was sound, and only enough to allow a single FFT to be performed.

The spectrogram for the same audio is shown.
Now the user can re-transcribe the session using any of the techniques available in the Audiophile’s Analyzer including the built in CNNs. This would simply not be possible in real time as it requires 7 FFTs to be performed before the spectrogram can be sliced and sent to the CNN.
The Audiophile’s Analyzer can also provide some insight into the internals of the Musician’s Workbench which are not normally displayed. Answering questions such as, “Should I have used Delayed Sampling?”, “Did I select the best Octave Range?”.
The problem with training neural networks is always finding the training data. Samples of individual notes are available on the internet. Samples of chords are not available.
There are 16 chord types that are recognized by the Audiophile’s Analyzer. There are 96 notes in 8 octaves. So, it is possible to play 1536 different cords on a piano keyboard. It is not practical to play, record and label so many samples.
To solve this a feature has been added to the CNN tab of the Audiophile’s Analyzer which will produce MIDI files for every possible chord for a selected instrument.

These MIDI files are then converted to .wav audio files using a third-party application. When read by the Audiophile’s Analyzer a spectrogram is produced.
The Training set creation utility is then used to slice the spectrogram to create the training images.

Monochrome images are used to train the CNN, color is for humans.
This utility will recognize the filename format and produce the labels file. Multiple labels will be applied to each file.

The Audiophile’s Analyzer is used to build and train a CNN using the labeled images.
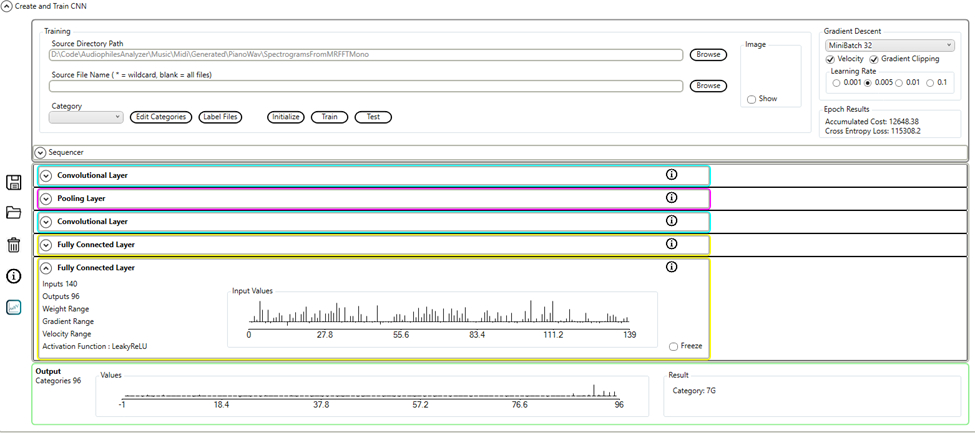
The output layer of the neural network will have 96 outputs, labeled from 0C to 7B. During training the required outputs will be set for each note in the file label.
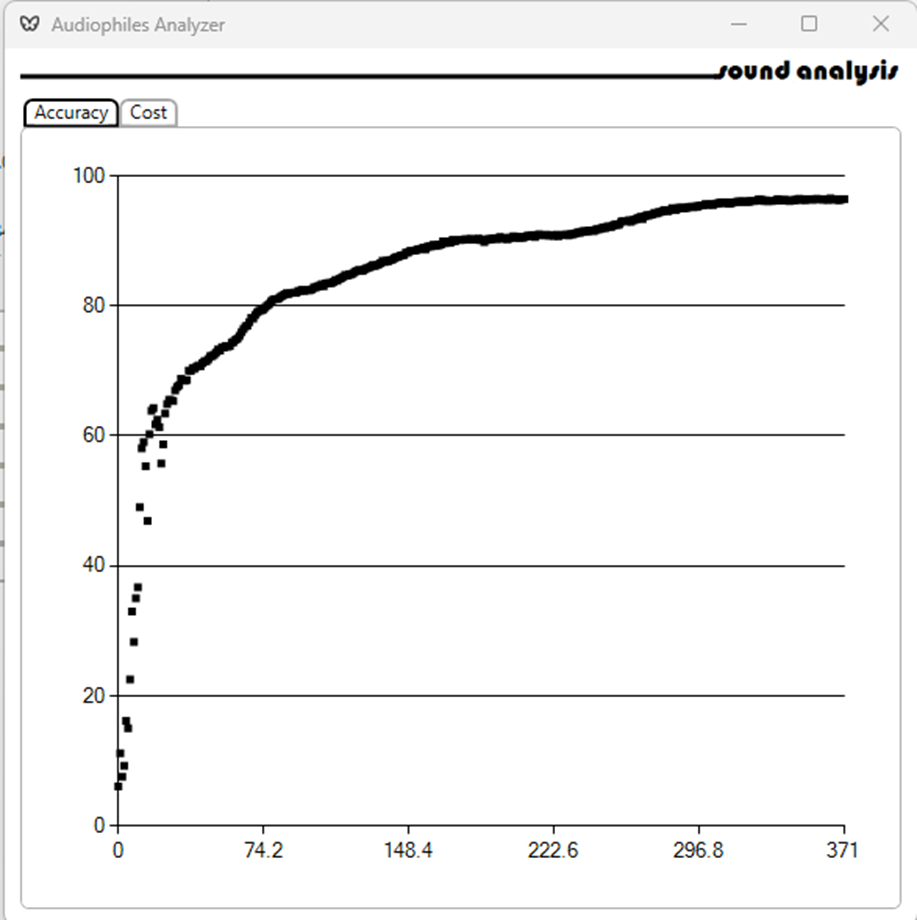
Training results are recorded:
Using the Audiophile’s Analyzer to transcribe a .wav file:
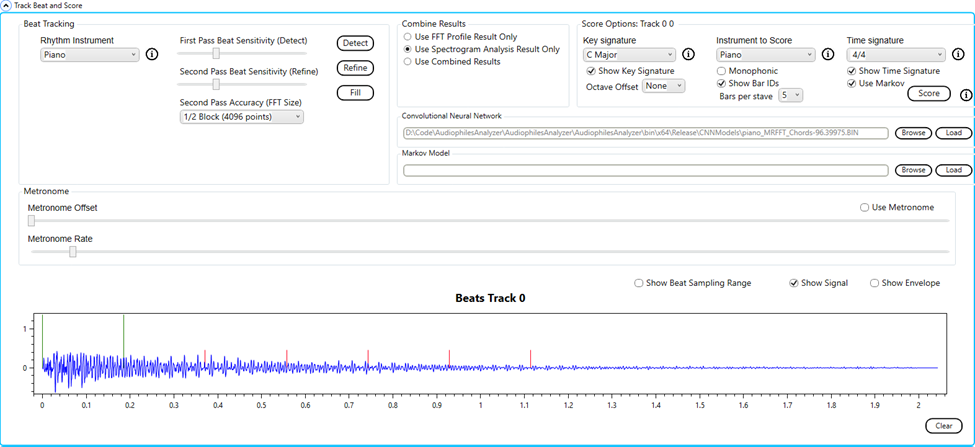

It can take a day or so to train a CNN model, or several minutes to create a profile, assuming that you have enough suitable samples. Fortunately it is possible to transcribe without prior training for a particular instrument. To illustrate this I have a single note played on a double bass (A octave 2).
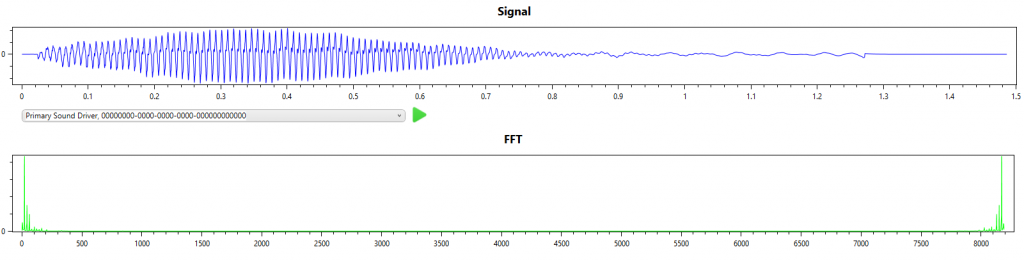
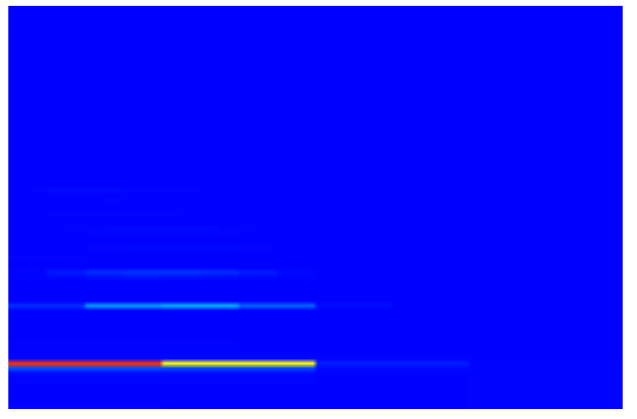
To transcribe I set the options to No Profile and Constant Q Mapping.
Selecting Use FFT Profile Result only
The result is

Selecting Use Spectrogram Analysis Result only I get

Here I perform the same task, i.e. single note (A2), this time from a cello. This is a little more difficult as the cello is a polyphonic instrument with very strong harmonics.
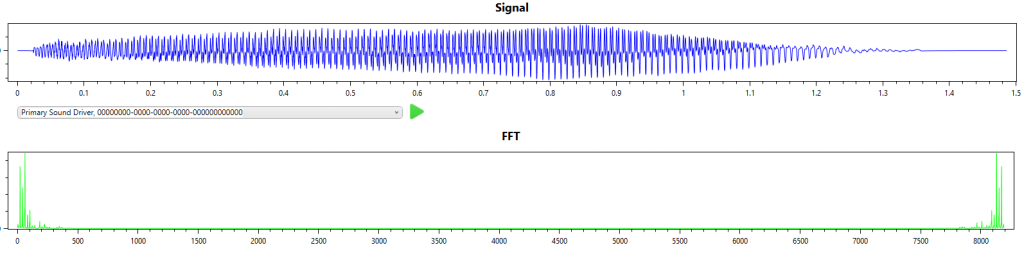
From the signal and FFT result we can see that the first overtone has more energy than the fundamental frequency.
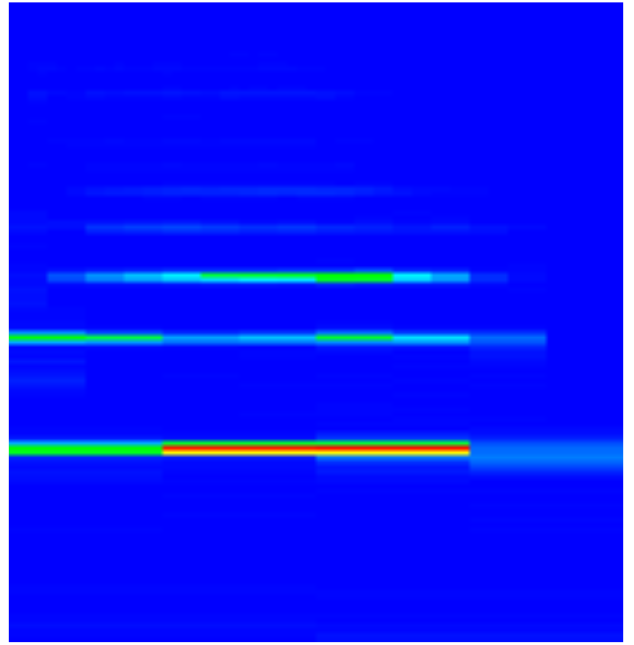
This problem is attenuated in the Multi-rate FFT spectrogram as the overtone is sampled over less time in the shorter sampled higher frequency FFT.
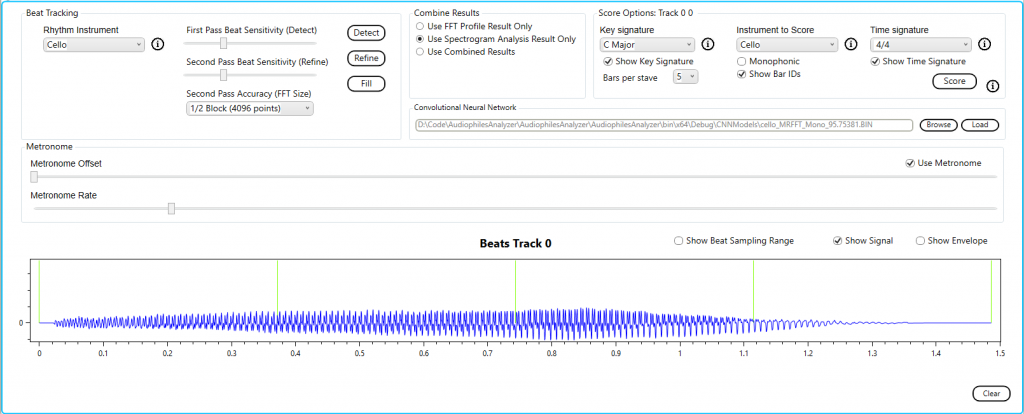
We use the built in profile for the cello.

Here we can see that as the note fades on the last beat the overtone is also transcribed.
Since we know that this was a single note the monophonic check box should be checked.

Now the result is as expected.

Using the built in Convolutional Neural Network for the cello we see leading and trailing silence; only the red line from the spectrogram has been transcribed.
The threshold for silence is calculated differently for the algorithm and the CNN. The algorithm sets the threshold on the fly during transcription based on a running average of the energy in the audio. For the CNN the threshold for silence is implemented when the spectrogram slices are prepared for training; the CNN was never trained on the parts of the note which were too quiet.
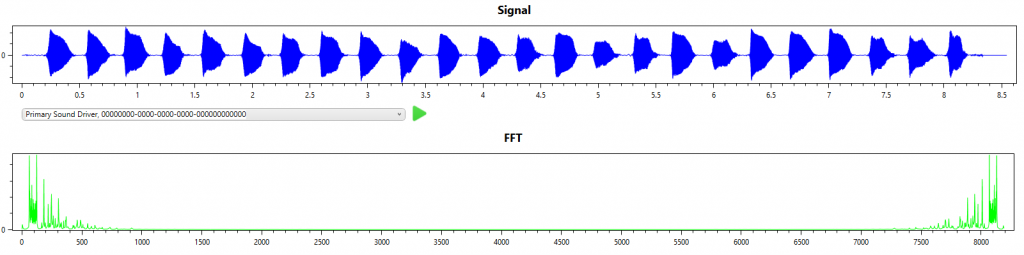
The simplest music file to transcribe is a single note. Here I use a bassoon playing a single note A (octave 2) to walk through the simplest transcription.
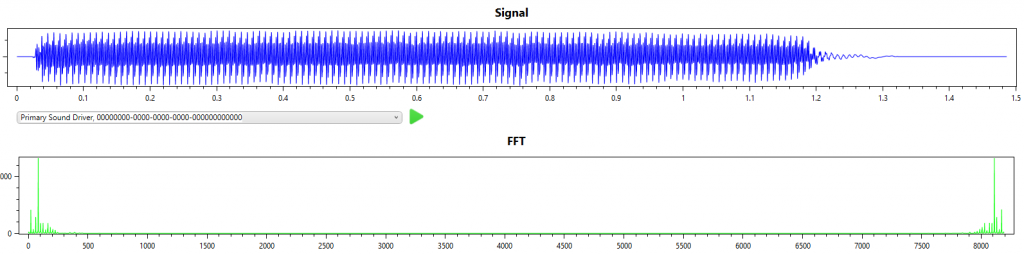
From the signal and FFT result we can see that this is indeed a single note with a single dominant frequency.
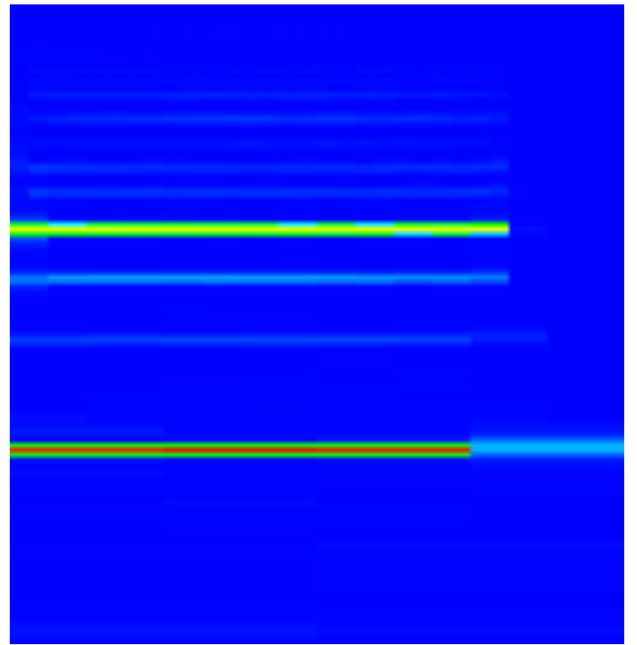
The spectrogram confirms the simplicity of this example.
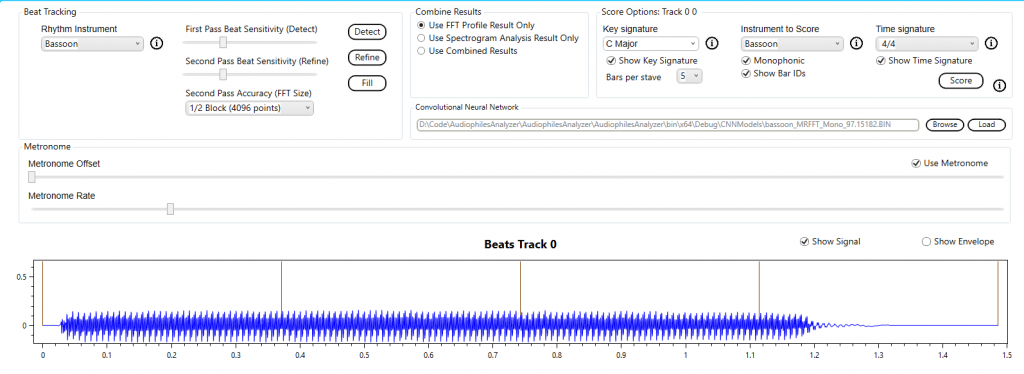
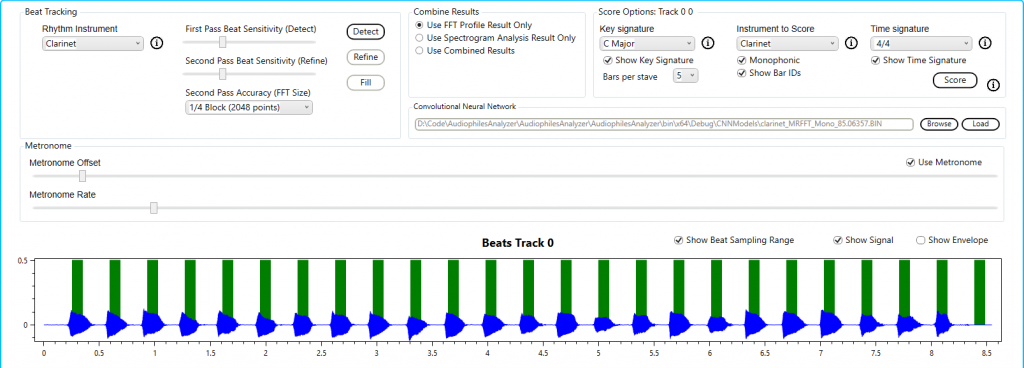
To transcribe this note we will use the built in bassoon profile and the default options (i.e. correlation).

The result is as expected.
Alternatively we could have elected to use the built in Convolutional Neural Network for the bassoon.

The result is a little different. The note ends just after the forth beat. The CNN transcribes this as a 3 beat note, not 4 beats.